New ice absorption coefficient in the visible and UV
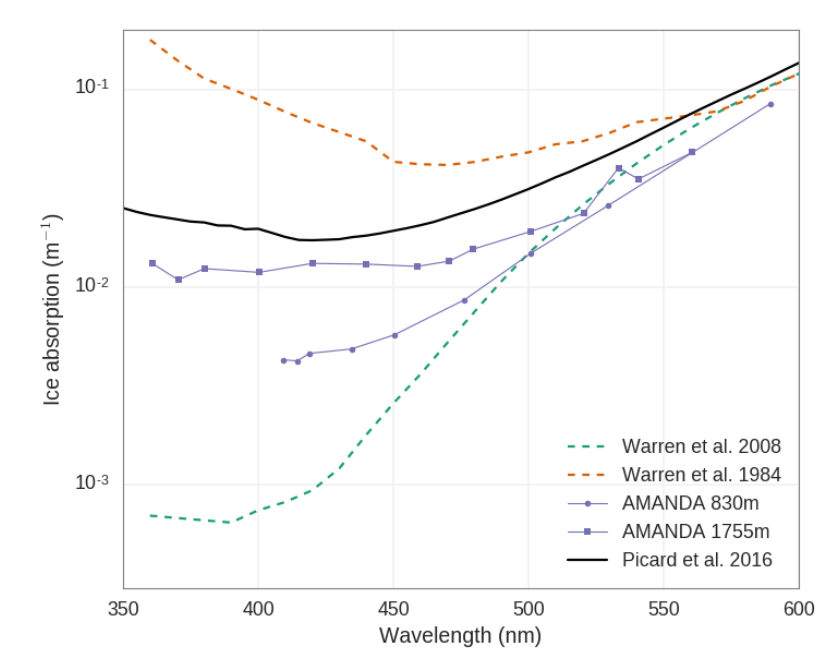
In Picard et al. 2016, we have estimated the ice absorption spectrum in the visible using many measurements of profile of radiance in snow. Our estimate is one order of magnitude larger than that of Warren et al. (2006) which is used in the most recent compilation of ice absorption (Warren and Brandt, 2008) in the wavelength range 200-600 nm. This is surprising because we use a similar experiment and method to that of Warren et al. (2006) and both experiments took place on the Antarctic Plateau near Dome C. However, we exploited many more measurements (77 homogeneous layers versus 1) which gives a statistical robustness to our results and even by analysing each indivual layer we did not find ice absorption as low as Warren et al. (2006). On the other hand our results are in better agreement with other estimates provided by the AMANDA group using a very different method. Our conclusion is that ice absorption in the visible is still uncertain, but it is unlikely to be as low as the estimates of Warren et al. (2006).
The new ice absorption and refractive index are provided in different format and in computer code:
- Ice absorption in simple ASCII format
- Refractive index imaginary part in simple ASCII format
- Refice Python code to compute the refractive index based on a merge between our estimate in the range 320-600 nm and Warren et al. (2008) compilation outside.
- Snowoptics, general purpose library for the snow optics computations that include the ice absorption function and much more. Just 'pip install snowoptics' and you're ready to work !
| Wavelength (nm) | Ice absorption (m-1) | Uncertainty (m-1) |
| 350 | 2.50e-02 | 8.61e-04 |
| 355 | 2.39e-02 | 8.40e-04 |
| 360 | 2.30e-02 | 7.67e-04 |
| 365 | 2.24e-02 | 7.86e-04 |
| 370 | 2.18e-02 | 7.92e-04 |
| 375 | 2.13e-02 | 7.12e-04 |
| 380 | 2.11e-02 | 7.35e-04 |
| 385 | 2.04e-02 | 7.52e-04 |
| 390 | 2.03e-02 | 7.42e-04 |
| 395 | 1.95e-02 | 6.96e-04 |
| 400 | 1.96e-02 | 6.81e-04 |
| 405 | 1.87e-02 | 6.76e-04 |
| 410 | 1.78e-02 | 6.38e-04 |
| 415 | 1.72e-02 | 5.93e-04 |
| 420 | 1.71e-02 | 6.36e-04 |
| 425 | 1.72e-02 | 6.21e-04 |
| 430 | 1.73e-02 | 6.31e-04 |
| 435 | 1.78e-02 | 5.98e-04 |
| 440 | 1.81e-02 | 6.96e-04 |
| 445 | 1.85e-02 | 6.36e-04 |
| 450 | 1.91e-02 | 6.50e-04 |
| 455 | 1.97e-02 | 6.99e-04 |
| 460 | 2.04e-02 | 7.43e-04 |
| 465 | 2.12e-02 | 7.48e-04 |
| 470 | 2.23e-02 | 7.98e-04 |
| 475 | 2.35e-02 | 8.38e-04 |
| 480 | 2.47e-02 | 8.85e-04 |
| 485 | 2.60e-02 | 8.77e-04 |
| 490 | 2.75e-02 | 9.19e-04 |
| 495 | 2.92e-02 | 1.05e-03 |
| 500 | 3.11e-02 | 1.08e-03 |
| 505 | 3.33e-02 | 1.16e-03 |
| 510 | 3.57e-02 | 1.19e-03 |
| 515 | 3.80e-02 | 1.35e-03 |
| 520 | 4.08e-02 | 1.37e-03 |
| 525 | 4.37e-02 | 1.50e-03 |
| 530 | 4.69e-02 | 1.56e-03 |
| 535 | 5.04e-02 | 1.69e-03 |
| 540 | 5.44e-02 | 1.78e-03 |
| 545 | 5.89e-02 | 1.97e-03 |
| 550 | 6.36e-02 | 2.16e-03 |
| 555 | 6.90e-02 | 2.29e-03 |
| 560 | 7.48e-02 | 2.44e-03 |
| 565 | 8.07e-02 | 2.83e-03 |
| 570 | 8.68e-02 | 2.95e-03 |
| 575 | 9.36e-02 | 3.12e-03 |
| 580 | 1.00e-01 | 3.38e-03 |
| 585 | 1.07e-01 | 3.70e-03 |
| 590 | 1.16e-01 | 3.97e-03 |
| 595 | 1.25e-01 | 4.32e-03 |
| 600 | 1.35e-01 | 4.56e-03 |